Comprendere gli alberi attraverso la matematica

Per la rubrica “Alberologia”, ho avuto il piacere di approfondire con il forestale Antonio De Bona il legame che unisce gli alberi, e la natura più in generale, ad una disciplina apparentemente un po’ ostica e, forse, il più delle volte ritenuta inutile e noiosa ma, a mio avviso, estremamente affascinante, proprio per il suo rigore e la sua complessità: la matematica.

Fin dalle sue origini, è stata considerata la scienza per eccellenza, la “scienza delle scienze”: in effetti, ogni disciplina scientifica o tecnica (dalla fisica all’ingegneria, dall’economia all’informatica) fa largo uso degli strumenti di analisi, di calcolo e di modellazione da essa offerti.

Già nell’Ottocento il filosofo francese, nonché fondatore del Positivismo, Auguste Comte, la considerava la scienza fondamentale, che consentiva a tutte le altre discipline di conseguire lo “stato positivo”. Le più antiche testimonianze delle conoscenze matematiche sono, però, ben più antiche (2500-3000 a.C.) e si trovano presso alcune civiltà preelleniche del Medio Oriente. Nei papiri egizi e nelle tavolette babilonesi sono stati rinvenuti calcoli, determinazioni di aree e volumi e risoluzioni di problemi di primo e secondo grado, a testimonianza del fatto che questi popoli si servivano già dell’aritmetica e della geometria per attività pratiche quali il commercio, l’agrimensura catastale (misurazione della terra), la navigazione e l’agricoltura.

Nei secoli il concetto di matematica “pura” (che studia i problemi matematici senza tenere in considerazione una loro possibile utilizzazione pratica) si è evoluto e modificato con l’intento di voler trovare soluzioni adatte a problemi concreti, attraverso l’elaborazione di strumenti e modelli utili agli scopi di scienze come la fisica, la chimica, la biologia.

Nei primi anni del Novecento, in particolare, hanno iniziato a prendere piede le applicazioni della matematica alla biologia, grazie ai lavori dei matematici Vito Volterra e Alfred J. Lotka sulle popolazioni interagenti, a cui seguirono lavori di altri matematici sulla genetica delle popolazioni, la diffusione delle epidemie, lo sviluppo, la neurobiologia…

Nonostante uno scetticismo iniziale da parte di alcuni biologi sulle effettive capacità della matematica di semplificare e di descrivere i sistemi biologici, dagli anni Sessanta in poi la biomatematica (anche detta biologia matematica) ha subìto una forte accelerata in seguito ad un interesse sempre maggiore verso questa disciplina, che ha aperto la strada a nuovi settori di ricerca.

Andando a ritroso nel tempo scopriamo, in realtà, che la matematica è stata utilizzata in biologia già nel XIII secolo, quando il matematico italiano Leonardo da Pisa, meglio noto come Fibonacci, per studiare la discendenza di una coppia di conigli ideò una successione di numeri interi, detta successione aurea (o di Fibonacci), in cui ogni elemento è uguale alla somma dei due precedenti: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89…

Fibonacci, inoltre, notò che il rapporto tra un numero della successione e quello immediatamente precedente si avvicinava sempre di più al numero irrazionale Φ (Phi) = 1,618…, il cosiddetto “numero aureo”, anche chiamato Sezione Aurea o Costante di Fidia. Questo rapporto è molto ricorrente in natura e lo si ritrova sotto forma di una spirale logaritmica (detta “spirale aurea”, in quanto ripete all’infinito le proporzioni della sezione aurea) osservando la geometria di piante, fiori e frutti, nelle conchiglie dei molluschi o, addirittura, negli alveari delle api. La successione di Fibonacci, in particolare, svolge un ruolo fondamentale nella fillotassi, che è proprio la branca della botanica che studia l’ordine con cui gli organi (foglie, rami, fiori o semi) di una specie vegetale sono disposti, in base alla ripetizione di pattern (schemi) regolari.

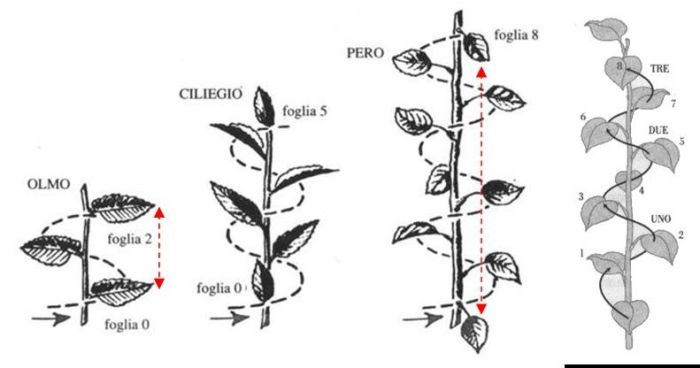
Keplero scoprì che su molti tipi di alberi le foglie sono allineate secondo uno schema che comprende due numeri di Fibonacci: partendo da una foglia qualunque, dopo uno, due, tre o cinque giri dalla spirale si trova sempre una foglia allineata con la prima e, a seconda delle specie, questa sarà la seconda, la terza, la quinta, l’ottava o la tredicesima.

I concetti di pattern e di simmetria sono molto diffusi in natura. Se pensiamo agli alberi, ci viene subito in mente la simmetria parte destra-parte sinistra, ricorrente nei disegni infantili, ma anche la simmetria radici-rami che si ritrova, invece, nei disegni più elaborati degli adulti. Osservando i tronchi e i rami in sezione trasversale possiamo notare un altro tipo di simmetria, quella radiale, che presuppone l’esistenza di un asse principale per il quale passano più piani di simmetria che dividono l’oggetto (in questo caso il tronco o i rami) in tante parti uguali e simmetriche tra loro.

L’albero di Pitagora è un esempio, invece, di una struttura a simmetria bilaterale (cioè con un unico piano di simmetria che divide l’oggetto in due parti uguali, perfettamente simmetriche) che richiama l’aspetto di un vero albero, ma non è altro che un frattale matematico: un quadrato ha un lato in comune con un triangolo rettangolo isoscele, che a sua volta ha gli altri due lati in comune con altri due quadrati e così via. La somma delle aree dei due quadrati più piccoli, per il teorema di Pitagora, è uguale all’area del quadrato iniziale e così anche le aree dei quadrati che si formano nei passaggi successivi, sommate, daranno l’area del primo quadrato. Costruendo un triangolo rettangolo qualsiasi sul lato del primo quadrato si può avere un albero asimmetrico la cui forma avvolta non è altro che una spirale logaritmica.

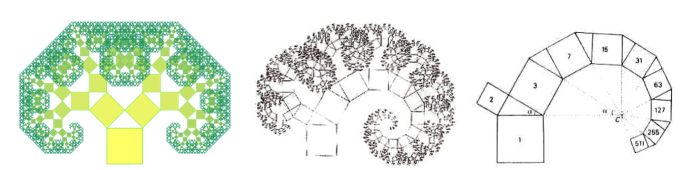
I frattali sono figure geometriche dotate di omotetia interna, cioè autosimili (ingrandendo una qualsiasi delle loro parti si ottiene una figura simile all’originale) che si ripetono all’infinito. Dal fiocco di neve alla coda del pavone, la natura è ricca di elementi frattali: basti pensare, per esempio, al broccolo romano, in cui il numero di rosette che lo compongono è sempre un numero della successione di Fibonacci o alla felce, in cui ogni singolo componente della foglia è simile alla foglia completa e ogni componente è, a sua volta, costituito da sub-componenti (piccole foglioline) simili al singolo componente e alla foglia completa.

500 anni fa Leonardo Da Vinci aveva capito che anche gli alberi sono di natura frattale: osservandone i rami, infatti, notò che quelli primari si ripetevano in strutture simili, più piccole, cioè i rami secondari. Nel suo taccuino scrisse che “tutti i rami di un albero in ogni stadio della sua altezza, quando messi insieme, hanno uno spessore uguale al tronco”: in altre parole, se i rami di un albero fossero piegati verso l’alto e schiacciati insieme, l’albero sembrerebbe un grande tronco con lo stesso spessore dall’alto verso il basso.

La teoria sugli alberi di Da Vinci è stata approfondita dal fisico francese Christophe Eloy in uno studio pubblicato nel 2011 sulla rivista Physical Review Letters, una delle più prestigiose riviste di fisica. Eloy ha condotto una serie di simulazioni per dimostrare che lo scheletro dell’albero ha una struttura autosimile e che i diametri dei rami si sono adattati a resistere alle sollecitazioni indotte dal vento con la minima biomassa. Alla fine, le simulazioni del fisico hanno confermato la regola di Da Vinci e quindi la teoria strutturale degli alberi che spiegherebbe la loro capacità di resistere agli stress; tuttavia, alcuni scienziati e ricercatori propendono maggiormente per la teoria idrologica, secondo la quale, invece, gli alberi avrebbero la loro forma caratteristica perché questa favorirebbe un trasporto più efficiente della linfa.

Sebbene ci siano ancora pochi dati sperimentali a sostegno delle osservazioni di Da Vinci, la sua teoria continua ancora oggi, dopo secoli, ad affascinare ed ispirare scienziati, ricercatori e artisti di tutto il mondo e lascia le porte aperte ad ulteriori ricerche che potrebbero svelarci nuove ed entusiasmanti scoperte sulla struttura delle foreste e sull’evoluzione degli alberi.

Ad oggi, per il tramite della matematica, siamo in grado di sapere quant’è alto un albero, di stimarne il volume (biomassa legnosa) in m³ e il tasso di accrescimento (incremento) nel tempo e, conseguentemente, di stimare il valore economico di un intero soprassuolo. In particolare, grazie ad operazioni di matematica finanziaria, che ci consentono di trasferire valori monetari nel tempo, siamo in grado di calcolare gli interessi che si vengono a maturare negli anni sul capitale iniziale (capitale legnoso).

L’esperto di economia agraria Arrigo Serpieri rilevò a riguardo come nella produzione forestale “i costi via via anticipati si fissino per lungo tempo nelle piante crescenti”; Duerr, nei suoi Fondamenti di economia forestale, definisce il capitale legnoso come una “macchina” che produce il legno, destinata essa stessa a diventare prodotto al momento del taglio (“il legno si produce dal legno”). Risulta facile, dunque, considerare il capitale legnoso come anticipazione di capitali, laddove si consideri la produzione forestale su base periodica, o come piante in piedi (parte del capitale fondiario) laddove si abbia una visione della produzione forestale su base annua, come nel caso di un bosco assestato, dotato di una provvigione (capitale legnoso) costante nel tempo.

Studiando le ampiezze degli anelli di accrescimento (dendrocronologia) di una singola pianta e le loro anomalie, inoltre, riusciamo a ricostruire la storia pregressa di tutto il bosco e quindi i periodi favorevoli, sfavorevoli e persino eventi come frane e alluvioni.

La matematica, dunque, attraverso una serie di formule e leggi più o meno complesse, ci aiuta a comprendere meglio gli equilibri e i meccanismi sui quali si fonda la natura e a guardarla con occhi nuovi, permettendoci di ammirare la sua infinita bellezza e, non di meno, la sua estrema fragilità.

“La matematica si può considerare come ciò che unisce e si interpone fra l’Uomo e la Natura, fra il mondo esterno e quello interno, fra il pensiero e la percezione.”
F. W. August Fröbel